ГОСТ ИСО 11843-3-2005 Статистические методы Способность обнаружения Методология определения критического значения отклика без использования данных калибровки

Статистические методы

СПОСОБНОСТЬ ОБНАРУЖЕНИЯ

Методология определения критического значения
отклика без использования данных калибровки

ISO 11843-3:2003

Capability of detection — Part 3: Methodology for determination of the critical
value for the response variable when no calibration data are used
(IDT)

Предисловие

Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-97 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Порядок разработки, принятия, применения, обновления и отмены»

Сведения о стандарте

1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО НИЦКД), Межгосударственным техническим комитетом по стандартизации МТК 125 «Статистические методы в управлении качеством продукции» на основе собственного аутентичного перевода стандарта, указанного в пункте 4

2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии

3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол № 28 от 9 декабря 2005 г.)

За принятие проголосовали:

(Поправка. ИУС 8-2007)

4 Настоящий стандарт идентичен международному стандарту ИСО 11843-3:2003 «Способность обнаружения. Часть 3. Методология определения критического значения отклика без использования данных калибровки» (ISO 11843-3:2003 «Capability of detection — Part 3: Methodology for determination of the critical value for the response variable when no calibration data are used»).

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ 1.5-2001 (подраздел 3.6)

5 Приказом Федерального агентства по техническому регулированию и метрологии от 18 августа 2006 г. № 168-ст межгосударственный стандарт ГОСТ ИСО 11843-3-2005 введен в действие в качестве национального стандарта Российской Федерации с 1 января 2007 г.

6 ВВЕДЕН ВПЕРВЫЕ

Информация о введении в действие (прекращении действия) настоящего стандарта публикуется в указателе «Национальные стандарты.

Информация об изменениях к настоящему стандарту публикуется в указателе «Национальные стандарты», а текст изменений — в информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе «Национальные стандарты»

Содержание

Введение

Идеальным требованием к способности обнаружения относительно выбранной переменной состояния является то, что с ее помощью действительное состояние исследуемой системы должно быть уверенно классифицировано либо как равное, либо как отличное от базового состояния системы. Однако из-за наличия систематических и случайных отклонений данное требование не может быть выполнено, так как в действительности все стандартные состояния, включая базовое состояние, никогда не могут быть выражены в абсолютных показателях переменной состояния. Следовательно, все состояния могут быть правильно охарактеризованы лишь в показателях отличий от базового состояния, т.е. в показателях приведенной переменной состояния.

Примечание — Руководство ИСО 30 и стандарт ИСО 11095 не делают различия между переменной состояния и приведенной переменной состояния. Следовательно, этими двумя документами стандартное состояние бездоказательно признано известным по отношению к переменной состояния.

Кроме того, калибровка и процессы отбора проб и выборки добавляют случайные изменения к результатам измерений.

 

Статистические методы

СПОСОБНОСТЬ ОБНАРУЖЕНИЯ

Методология определения критического значения отклика
без использования данных калибровки

Statistical methods. Capability of detection. Methodology for determination of the critical value
for the response variable when no calibration data are used

1 Область применения

Настоящий стандарт содержит описание метода оценки критического значения отклика* на основе среднего и стандартного отклонения при повторных измерениях стандартного состояния в некоторых ситуациях (см. ), в которых значение приведенной переменной состояния равно нулю. Следовательно, можно сделать вывод о том, выходят ли значения отклика в действительном состоянии (исследуемая проба) за диапазон значений в стандартном состоянии.

Общие процедуры для определения критических значений отклика, приведенной переменной состояния, минимального обнаруживаемого значения описаны в ИСО 11843-2. Эти процедуры применяют в ситуациях, когда существует соответствующая функция калибровки**, а стандартное отклонение остатка измеренных откликов либо постоянно, либо представляет собой линейную функцию, зависящую от приведенной переменной состояния. Процедура определения критического значения отклика, приведенная в настоящем стандарте, рекомендована для применения лишь в случаях, когда не используют данные калибровки.

Процедура, описанная в настоящем стандарте, рекомендована для применения в ситуациях, когда трудно получить большое количество действительных состояний, несмотря на то, что может быть подготовлено большое количество базовых состояний.

___________________

* Выходная переменная (см. ИСО 3534-3, подраздел 1.2).

** Аналогом функции калибровки в национальных стандартах Российской Федерации является градуировочная кривая.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ИСО 3534-1:1993 Статистика. Словарь и условные обозначения. Часть 1. Вероятность и основные статистические термины

ИСО 3534-2:1993 Статистика. Словарь и условные обозначения. Часть 2. Статистическое управление качеством

ИСО 3534-3:1999 Статистика. Словарь и условные обозначения. Часть 3. Планирование экспериментов

ИСО 5479:1997 Статистическое представление данных. Проверка отклонения распределения вероятностей от нормального распределения

ИСО 11095:1996 Калибровка линейная с использованием образцовых материалов

ИСО 11843-1:1997 Способность обнаружения. Часть 1. Термины и определения

ИСО 11843-2:2000 Способность обнаружения. Часть 2. Методология в случае линейной калибровки

ИСО Руководство 30:1992 Термины и определения, касающиеся эталонных материалов

3 Термины и определения

В настоящем стандарте применены термины по ИСО 3534-1, ИСО 3534-2, ИСО 3534-3, ИСО Руководство 30, ИСО 11095 и ИСО 11843-1.

4 Планирование экспериментов

4.1 Общие положения

Предполагают, что метод измерений стандартизован. Известно, что метод калиброван для проведения подобных измерений, однако калибровка в конкретных условиях и при очень малых значениях приведенной переменной состояния либо не проводилась, либо была невозможна. Такой же метод измерений должен быть использован для всех повторных измерений стандартного состояния, в котором переменная состояния равна нулю, а также для действительных состояний (исследуемые образцы) в пределах совокупности измерений, для которой определено требуемое критическое значение отклика.

Измерения в действительности должны быть распределены случайным образом вокруг базового состояния.

Отрицательные значения отклика, если таковые появляются, не следует отбрасывать или изменять. Например, отрицательные значения нельзя заменять нулями.

4.2 Выбор стандартного состояния, при котором значение приведенной переменной состояния равно нулю

Одним из допущений в процедуре, описанной в настоящем стандарте, является то, что значение приведенной переменной состояния равно нулю в выбранном стандартном состоянии. Ожидаемая точность в этом случае рассмотрена в ИСО 11843-2, подраздел 4.1. На практике стандартные состояния известны не в абсолютных значениях переменной состояния, а только в значениях отклонений от базового (гипотетического) состояния. Что касается настоящего стандарта, достаточно, чтобы эталонный уровень был значительно ниже значения, измеряемого используемым методом.

В случаях, когда базовое состояние зависит от качества подготовки стандартного образца, его состав должен как можно более соответствовать составу измеряемого материала, т.е. в аналитической химии выбранный холостой основной материал должен по всем параметрам быть или подобным, или идентичным образцам исследуемой серии измерений. Влияние других веществ или элементов, присутствующих в образце, а также его физического состояния может быть очень значительным. В частности, при исследовании растворов невозможно использовать чистые растворители взамен экстрактов селективной сольвентной очистки, обычно предусматриваемых методом измерений.

4.3 Повторение эксперимента

4.3.1 Количество повторений J

При использовании данного метода для базового состояния для получения точных оценок среднего и стандартного отклонения отклик должен быть измерен на основе достаточно большого числа J повторений всей процедуры. Для исследования вида распределения данных и отнесения распределения отклика к нормальному или близкому к нормальному распределению необходимо наличие достаточного объема данных. Обычно 30 измерений достаточно, чтобы оценка стандартного отклонения отличалась не более чем на 30 % от истинного стандартного отклонения с вероятностью, близкой к 95 %.

Примечание — В некоторых ситуациях невозможно провести указанное выше количество измерений из-за ограничений на количество доступного материала или по другим причинам. В подобных ситуациях полученная оценка стандартного отклонения является недостоверной. Когда необходимо получить такую оценку s (см. s_b в ) истинного стандартного отклонения σ, можно утверждать, что интервал, основанный на s, накрывает σ с заданной вероятностью 1 — α. Такой статистический интервал (доверительный интервал для величины σ) определяют (при условии, что действует предположение о нормальности распределения и s является выборочным стандартным отклонением), используя распределение хи-квадрат:

гдe v = J — 1;

α — ошибка первого рода (см. введение).

Значения квантилей χ²-распределения можно получить из стандартных таблиц.

Повторение измерений (K — количество повторений) действительного состояния (исследуемого образца) позволяет до некоторой степени снизить критическое значение отклика [см. формулу ()], хотя для этого необходимо тщательно изучить возможные финансовые ограничения.

4.3.2 Однотипность повторений

При отборе проб базового состояния для измерения отклика необходимо полностью следовать процедуре отбора проб в пределах общего метода.

Если доступны стандартные образцовые вещества, то следует использовать их, поскольку однородность этих образцов уже была тщательно исследована.

Возможности проявления некоторых поверхностных факторов, таких как электростатическое влияние, осаждение, приводящих к неидентичности образцов, следует всегда принимать во внимание.

4.3.3 Возможные факторы негативного влияния

Изменение возможных факторов негативного влияния во время измерений должно быть минимизировано (см. ИСО 11843-2, подраздел 4.1).

5 Расчет критического значения отклика ус

5.1 Основной метод

В соответствии с ИСО 11843-1 критическое значение у_с — это такое значение отклика у, при превышении которого делают вывод о том, что система не находится в базовом состоянии. Критическое значение выбирают таким образом, что при нахождении системы в базовом состоянии подобный вывод возможен лишь с небольшой вероятностью а, т.е. критическое значение является минимальным значимым значением измерения или сигнала, используемым для его выделения по отношению к фону (шуму).

Решение «обнаружено» или «не обнаружено» принимают путем сравнения арифметического среднего результатов измерений, полученных для действительного состояния , с критическим значением у_с соответствующего распределения. Вероятность того, что арифметическое среднее измеренных значений  превысит критическое значение у_с для распределения в базовом состоянии (х = 0), должна быть не больше заданной вероятности α.

Для критического значения у_с справедливо неравенство:

                                                                                              (1)

Примечание —  обозначает вероятность того, что  при условии х = 0.

Для непрерывного распределения неравенство (1) может переходить в равенство, а для дискретного распределения (например, пуассоновского распределения), для которого не все значения α возможны, неравенство (1) имеет вид строгого неравенства.

Если выполнены следующие условия:

a) у имеет нормальное распределение со стандартным отклонением σ₀,

b) образцы в действительном состоянии максимально однородны,

c) измерения объективны, —

критическое значение отклика вычисляют по упрощенной формуле (1)

                                                                                           (2)

где  — квантиль нормированного нормального распределения уровня 1 — α;

 — стандартное отклонение холостого сигнала (или концентрации) нулевой гипотезы (истинное значение х = 0);

J — количество повторений определения базового состояния;

 — арифметическое среднее повторений определения базового состояния;

K — количество определений действительного состояния.

Примечание — В формуле (2) знак «+» используют тогда, когда значение отклика увеличивается с повышением уровня приведенной переменной состояния, а знак «-» используют тогда, когда значение отклика уменьшается с повышением уровня приведенной переменной состояния.

Если в качестве оценки  используют s₀, квантиль  заменяют соответствующим квантилем t-распределения Стьюдента с v степенями свободы, т.е.

                                                                                         (3)

Примечание — В формуле (3) знаки «+» и «-» используют так же, как в формуле (2).

Если известно, что значение переменной состояния в базовом состоянии для любых обозримых и разумных целей равно нулю, т.е. «базис» для отклика известен с незначительной ошибкой, то  =  и в качестве оценки для  используют стандартное отклонение повторных определений отклика в базовом состоянии s_b. Этот способ получения экспериментальной оценки  рассмотрен в настоящем стандарте.

5.2 Практические вычисления

Повторяющиеся измерения отклика в базовом состоянии должны быть исследованы на согласованность с нормальным распределением с помощью методов, приведенных в ИСО 5479, или других методов.

Для целей настоящего стандарта выполняют J повторений измерения отклика в базовом состоянии в пределах серии измерений. Таким образом, выборочное среднее у, вычисляемое по формуле

является оценкой математического ожидания у₀ для у, а выборочное стандартное отклонение у, вычисляемое по формуле

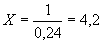
является оценкой .

Оценку критического значения отклика вычисляют следующим образом:

                                                                                         (4)

где число степеней свободы v = J — 1. Статистический критерий является односторонним, α обычно приравнивают 0,05, как это рекомендовано ИСО 11843-1, а соответствующий квантиль t-распределения Стьюдента определяют по стандартным таблицам.

Примечание — В формуле (4) знаки «+» и «-» используют так же, как и в формуле ().

Формулу (5) применяют непосредственно в ситуации, когда выполняют единственное определение на исследуемом образце:

                                                                                            (5)

Примечание — В формуле (5) знаки «+» и «-» используют так же, как и в формуле ().

5.3 Составление отчета

Количество измерений отклика в базовом состоянии J, а также стандартное отклонение s_b должны быть зафиксированы для данной серии измерений. Количество повторений для отклика в действительном состоянии K также должно быть зафиксировано в отчете. Кроме того, в отчете должны быть зафиксированы выбранное значение α (обычно принимают 0,05), критическое значение, вычисленное для установленного количества повторений для отклика в базовом и действительном состояниях. Все вышеперечисленные параметры приведены в таблице 1.

Если среднее из K повторных определений в действительном состоянии не превышает критического значения, можно утверждать, что между действительным и базовым состояниями нет различия.

Однако среднее для действительного состояния должно быть приведено в отчете в соответствии с фактическими расчетами, а не приравнено нулю.

Таблица 1 — Критическое значение отклика и соответствующие экспериментальные данные

Количество повторений для отклика в базовом состоянии	J
Количество повторений для отклика в действительном состоянии	K
Выбранное значение α (значение по умолчанию 0,05)	α
Среднее значение отклика в базовом состоянии
Среднее значение отклика в действительном состоянии
Стандартное отклонение отклика в базовом состоянии	sb
Критическое значение отклика, полученное упрощенным методом, описанным в настоящем стандарте, без использования данных калибровки	yc

Приложение А
(обязательное)

Используемые обозначения

b₂ — тестовая статистика для эксцесса,

J — количество повторений измерений отклика в базовом состоянии, когда переменная состояния равна нулю (холостая проба).

j = 1, 2,…,J — переменная, соответствующая действиям, осуществляемым в базовом состоянии, когда переменная состояния равна нулю (холостая проба).

K — количество повторений измерений отклика в действительном состоянии (образец).

Р — вероятность.

s — оценка стандартного отклонения отклика.

s_b -оценка стандартного отклонения отклика, когда переменная состояния равна нулю (холостая проба).

s₀ — оценка стандартного отклонения измеренного отклика в базовом состоянии.

t — статистика распределения Стьюдента.

W — тестовая статистика критерия Шапиро-Уилкса.

x — значение приведенной переменной состояния.

у — значение отклика.

 — арифметическое среднее измеренных откликов в базовом состоянии.

 — арифметическое среднее измеренных откликов в действительном состоянии (образец).

у_с — критическое значение отклика.

y_j -значение j-го измерения отклика на конкретном уровне и в конкретной серии.

у₀ — математическое ожидание отклика при нулевом значении переменной состояния.

 — квантиль нормального распределения уровня (1 — α).

α — уровень значимости или вероятность ошибки первого рода (вероятности ошибочного обнаружения того, что система вышла из базового состояния, когда в действительности она находится в базовом состоянии).

1 — α — уровень доверия.

v = J — 1 — степени свободы t-статистики или х²-статистики.

σ — истинное стандартное отклонение.

σ₀ — истинное стандартное отклонение отклика в базовом состоянии.

σ_b — истинное стандартное отклонение отклика при нулевом значении переменной состояния (холостая проба).

χ² — случайная величина с распределением хи-квадрат.

Приложение В
(справочное)

Примеры

В.1 Пример 1

Измерение массовой доли кадмия в пробе грунта BCR с использованием атомной эмиссии после настаивания в царской водке

Пробы стандартного образца легкого песчаного грунта CRM 142 массой 0,5 г были проанализированы на содержание кадмия. По другим данным известно, что реальное содержание кадмия не превышает критического предела, присущего используемому методу измерений (составляет примерно 1/10 критического уровня). Пробы были одновременно настоены в царской водке (групповая технология), отфильтрованы, и их объем доведен до 25 см³ для спектроскопии. Было проведено J = 30 считываний в пределах одной серии измерений с использованием 24-канального спектрометра с индуктивно связанной плазмой, измеряющего массовую долю кадмия при длине волны на уровне 226 нм, и с последующей корректировкой на смещение.

Таблица В.1 — Результаты эмиссионного спектрального анализа кадмия при длине волны 226 нм проб образца грунта CRM 142

После проведения нескольких тестов на обнаружение отличий от нормального распределения (асимметрия, эксцесс, критерий Шапиро-Уилкса) и выявления резко выделяющихся значений был сделан вывод о том, что нет значительного отклонения от нормального распределения.

Значение квантиля Стьюдента (односторонний интервал) для 29 степеней свободы и α = 0,05 в соответствии со стандартными таблицами: t_1-α (v) = t_0,95 (29) = 1,699.

Среднее значение откликов  = 2,1898 мB, стандартное отклонение s_b = 0,0186 мB.

Три повторных измерения были выполнены одновременно на подобном образце грунта и были получены отклики: 2,177; 2,183 и 2,161 мB.

В соответствии с формулой () было рассчитано критическое значение отклика трех повторных измерений для фактического образца с точностью до трех десятичных знаков после запятой:

Полученные результаты приведены в таблице В.2.

Таблица В.2 — Критическое значение отклика для кадмия, полученное с использованием атомной эмиссии при длине волны 226 нм из образца грунта CRM 142

Количество повторений для отклика в базовом состоянии	30
Количество повторений для отклика в действительном состоянии	3
Выбранное значение α (значение по умолчанию 0,05)	0,05
Среднее значение отклика в базовом состоянии	2,1898 мB
Среднее значение отклика в действительном состоянии	2,1737 мB
Стандартное отклонение отклика в базовом состоянии	0,0186 мB
Критическое значение отклика, полученное упрощенным методом, описанным в настоящем стандарте, без использования данных калибровки	2,209 мB

Критическое значение отклика не было превышено, нет различия между базовым состоянием и опытным образцом.

Примечание — Полученное критическое значение намного больше значения для полного процесса с использованием только реагентов (такое значение — 0,815 мB) и намного больше значения, заявленного производителем прибора для определения содержания ионов кадмия в «чистом» водном растворе (такое значение — примерно 0,027 мB).

В.2 Пример 2

Определение химического потребления кислорода водой с использованием титриметрического метода

Необходимо отметить, что функция калибровки* для данной процедуры измерений химического потребления кислорода водой является монотонно убывающей: по мере увеличения объема потребления кислорода водой объем свободного кислорода уменьшается и, соответственно, уменьшается объем раствора железоаммонийных квасцов [железо (III) аммоний сульфат], использованный в процессе титрования.

Для определения химического потребления кислорода водой (в миллилитрах) в процессе титрования с использованием 0,060 моль/л раствора железоаммонийных квасцов было измерено 30 холостых проб (см. таблицу в.3).

Таблица В.3 — Определение химического потребления кислорода водой титриметрическим методом

После проведения нескольких испытаний на выявление отклонений от нормального распределения (асимметрия, эксцесс, критерий Шапиро-Уилкса) и выявления резко выделяющихся значений (единичный критерий Граббса, двойной критерий Граббса) был сделан вывод, что есть незначительное отклонение от нормального распределения: критерий для эксцесса не выполняется при α = 0,01 (b₂ = 1,737 против критических значений 1,79 и 5,12), а критерий Шапиро-Уилкса не выполняется для α = 0,05 (W = 0,9045 против критических значений 0,900 при α = 0,01 и 0,927 при α = 0,05). Распределение исходных данных может быть описано как близкое к нормальному, поскольку результаты двух тестов указывают на нормальное распределение. Однако даже частотная диаграмма распределения указывает на возможность того, что результаты принадлежат двум распределениям. Следовательно, на практике необходимо убедиться в том, что в лаборатории, приводящей данные по откликам, нет ошибок при выполнении записей. Если делают вывод о правильной регистрации данных, критическое значение отклика при однократном измерении действительного состояния (опытного образца) рассчитывают следующим образом:

Среднее значение откликов равно  = 19,829 см³, а стандартное отклонение s_b = 0,0774 см³.

Значение квантиля распределения Стьюдента (односторонний интервал) для 29 степеней свободы и α = 0,05 определено по стандартным таблицам: t_1-α (v) = t_0,95(29) = 1,699.

В соответствии с формулой (), поскольку функция калибровки* убывает, требуется использовать знак «-», а не «+». Следовательно, критическое значение отклика с точностью до двух десятичных знаков после запятой для единичных измерений опытного образца имеет вид:

Полученные результаты приведены в таблице В.4.

__________________

* Аналогом функции калибровки в национальных стандартах Российской Федерации является градуировочная кривая.

Таблица В.4 — Критические значения отклика для определения химического потребления кислорода водой титриметрическим методом

Количество повторений для отклика в базовом состоянии	30
Количество повторений для отклика в действительном состоянии	1
Выбранное значение α (значение по умолчанию 0,05)	0,05
Среднее значение отклика в базовом состоянии	19,829 см3
Стандартное отклонение отклика в базовом состоянии	0,0774 см3
Критическое значение отклика, полученное упрощенным методом, описанным в настоящем стандарте, без использования данных калибровки	19/70 см3

Поскольку объем 0,060 моль/дм³ раствора железоаммонийных квасцов [железо (III) аммоний сульфат], израсходованный в процессе титрования, для действительного состояния (опытного образца) не ниже 19,70 см³, нет различия между базовым состоянием и опытным образцом.

Приложение С
(справочное)

Сведения о соответствии межгосударственных стандартов ссылочным международным стандартам