ГОСТ Р 51901-14-2007 Менеджмент риска Структурная схема надежности и булевы методы

Менеджмент риска

СТРУКТУРНАЯ СХЕМА НАДЕЖНОСТИ И БУЛЕВЫ МЕТОДЫ

IEC 61078:2006
Analysis techniques for dependability — Reliability block diagram and boolean methods (MOD)

Предисловие

Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации — ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»

Сведения о стандарте

1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») на основе собственного аутентичного перевода стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 10 «Перспективные производственные технологии, менеджмент и оценка рисков»

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря 2007 г. № 569-ст

4 Настоящий стандарт является модифицированным по отношению к международному стандарту МЭК 61078:2006 «Методы анализа надежности систем. Структурная схема надежности и булевы методы» (IEC 61078:2006 «Analysis techniques for dependability — Reliability block diagram and boolean methods») путем внесения технических отклонений, объяснение которых приведено во введении к настоящему стандарту.

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5)

5 ВЗАМЕН ГОСТ Р 51901.14-2005 (МЭК 61078:1991)

Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет

Содержание

Введение

Существуют различные методы построения структурной схемы надежности (RBD¹)). Цель применения каждого из этих методов и возможность их индивидуального или комбинированного применения для оценки показателей безотказности и готовности системы или ее компонентов должны быть определены до начала работы над RBD. Необходимо также провести анализ результатов каждого метода, требуемых данных, сложности метода и других факторов, указанных в настоящем стандарте.

RBD представляет собой графическое изображение работоспособного состояния системы. RBD показывает логическую связь функционирующих компонентов, необходимых для успешной работы системы (далее — успех системы).

В отличие от применяемого международного стандарта в настоящий стандарт не включены ссылки на МЭК 60050-191:1990 «Международный электротехнический словарь. Глава 191. Надежность и качество услуг», который нецелесообразно применять в национальном стандарте из-за отсутствия принятого гармонизированного национального стандарта. Ссылки на национальные стандарты выделены в тексте стандарта курсивом.

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Дата введения — 2008-09-01

1 Область применения

Настоящий стандарт устанавливает методы построения модели надежности системы и использования этой модели для вычисления показателей ее безотказности и готовности.

Методы моделирования на основе структурной схемы надежности предназначены для невосстанавливаемых систем, у которых порядок появления отказов не имеет значения. Для систем, у которых порядок появления отказов должен учитываться, и восстанавливаемых систем более подходящими являются другие методы, такие как Марковский анализ.

Следует отметить, что для целей настоящего стандарта термины «блок» и «элемент» являются идентичными и обозначают группу из одного или нескольких компонентов системы, рассматриваемую как неделимое целое.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения

ГОСТ Р 51901.13-2005 (МЭК 61025:1990) Менеджмент риска. Анализ дерева неисправностей

Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены термины и определения по ГОСТ Р 50779.10.

4 Условные обозначения

В настоящем стандарте применены следующие обозначения:

А, В, С — при использовании в булевых выражениях указывают на то, что объекты А, В, С находятся в работоспособном состоянии;

 — при использовании в булевых выражениях указывают на то, что объекты А, В, С находятся в неработоспособном состоянии;

F_s — вероятность отказа системы;

f_A(t) — плотность распределения наработок до отказа блока А;

P(SS|отказ X) — условная вероятность успеха системы при условии, что объект X отказал;

R, R(t), R_s(t) — вероятность безотказной работы [вероятность того, что объект может выполнять требуемую функцию в заданных условиях в течение интервала времени (0, f)];

R_A, R_B, … — вероятность безотказной работы блоков А, В,…;

R_s — вероятность безотказной работы системы;

R_sw — вероятность безотказной работы устройств переключения и датчиков;

SF — отказ системы (используется в булевых выражениях);

SS — успех системы (используется в булевых выражениях);

t — заданная наработка или рассматриваемый период времени;

λ_A, λ_B, λ_C — постоянная интенсивность отказов блоков А, В и С;

λ_Bd — интенсивность отказов блока В, находящегося в состоянии ненагруженного резерва;

μ_A, μ_B, μ_C — постоянная интенсивность ремонта блоков А, В и С;

 — количество способов выбора r объектов из n (число сочетаний из n по r);

0, 1 — символы, используемые в таблицах истинности для обозначения отказа и работоспособного состояния объекта, а также в заголовках колонок таблиц;

,. — символы булевой алгебры, обозначающие логическое И, например А  В, А.В = АВ (пересечение А и В);

   ,+ — символы булевой алгебры, обозначающие логическое ИЛИ, например А  В, А. + В (объединение А и В);

 

 

 

 

Примечание — Такие обозначения используются только для удобства. Они не обязательны, но могут быть полезны в случаях, когда направление имеет значение;

5 Предположения и ограничения

5.1 Независимость событий

Одним из самых важных предположений, на котором основан метод, установленный в настоящем стандарте, является то, что элементы системы (или блоки, их представляющие в RBD) могут существовать только в одном из двух состояний: работоспособном или неработоспособном (отказ).

Другим важным предположением является то, что отказ (или ремонт) любого блока не влияет на вероятность отказа (или ремонта) любого другого блока системы. Это означает, что имеются достаточные ресурсы для обслуживания блоков, нуждающихся в ремонте, и что любое необходимое количество специалистов может заниматься восстановлением конкретного блока одновременно, не мешая друг другу. Таким образом, предполагается, что отказы и ремонт отдельных блоков являются статистически независимыми событиями.

5.2 Последовательные события

Метод RBD не подходит для моделирования событий, зависящих от порядка их появления или зависимых во времени. В таких случаях необходимо использовать другие методы, например Марковский анализ или сети Петри.

5.3 Распределение наработок до отказа

Если выполняются предположения, указанные в 5.1, нет других ограничений для распределения, используемого для описания наработок до отказа или ремонта.

6 Определение состояний успеха/отказа системы

6.1 Общие положения

Основой для построения модели безотказности системы является четкое понимание вариантов функционирования системы. Часто для системы необходимо несколько определений успеха/отказа. Все они должны быть определены и перечислены. RBD может быть построена на различных уровнях: уровне системы в целом, уровне подсистемы/модуля или уровне сборочных единиц. Если RBD разрабатывают для дальнейшего анализа системы (например, для применения FMEA¹)), должен быть выбран уровень, подходящий для такого анализа.

Кроме того, должны быть четко описаны:

— выполняемые функции;

— эксплуатационные параметры и их допустимые предельные значения;

— условия эксплуатации и окружающей среды.

При разработке RBD допускается использовать методы качественного анализа. Поэтому должно быть установлено определение для успеха/отказа системы. Для каждого определения успеха/отказа системы на следующем этапе систему необходимо разделить на логические блоки в соответствии с целями анализа. Блоки могут представлять собой подсистемы, которые в свою очередь могут быть представлены собственными RBD (восстанавливаемых систем, см. ).

Для определения количественных оценок показателей безотказности на основе RBD применимы различные методы. В зависимости от вида структурной схемы надежности используют простые булевы методы (см. ) и/или анализ дерева неисправностей (см. ГОСТ Р 51901.13). Вычисления могут быть сделаны с применением методов теории надежности, аналитических методов или моделирования Монте-Карло. Преимущество моделирования Монте-Карло заключается в том, что события в соответствии с RBD не должны быть описаны аналитически, так как моделирование учитывает лишь состояние (работоспособное или неработоспособное) каждого блока (см. ).

Так как структурная схема надежности описывает логические отношения, необходимые для описания функционального состояния системы, она не обязательно отражает способ физического соединения аппаратных средств, хотя RBD обычно в максимально возможной степени учитывает физические связи в системе.

¹⁾ Failure for mode and effects analysis (FMEA) — анализ видов и последствий отказов.

6.2 Детальные рассмотрения

6.2.1 Функционирование системы

Возможно, что рассматриваемый объект функционирует в нескольких режимах. Если для каждого режима используют отдельную систему, то каждый такой режим необходимо рассматривать независимо от других и использовать при этом свои модели функционального состояния системы. Если все функции выполняет одна система для каждого типа функционирования, следует использовать свою RBD. При этом необходимо наличие четких описаний (логических утверждений) успеха/отказа системы для каждой ее функции.

6.2.2 Условия окружающей среды

Требования к функционированию системы должны сопровождаться описанием внешних условий, для которых разработана система. В описание внешних условий должно быть включено описание условий, воздействию которых система будет подвергаться при транспортировании, хранении и эксплуатации.

Обычно часть оборудования предназначена для использования в нескольких внешних условиях. Например, на морском судне, в самолете или на земле. В этом случае оценки показателей безотказности могут быть выполнены с помощью одной и той же структурной схемы надежности и интенсивностей отказов, соответствующих каждой внешней среде.

6.2.3 Рабочий цикл

Должны быть установлены соотношения между календарным временем, наработками и циклами включения/выключения. Если предполагают, что процесс включения/выключения оборудования не порождает отказов и интенсивность отказов оборудования при хранении является несущественной, то следует учитывать только фактическое время работы оборудования.

Однако в некоторых случаях процессы включения и выключения являются главной причиной отказа оборудования. Кроме того, оборудование может иметь более высокую интенсивность отказов при хранении чем при работе (из-за воздействия влажности, коррозии и др.). В сложных случаях, когда только части системы включаются и выключаются, более подходящими для моделирования являются другие методы (например, Марковский анализ).

7 Простые модели

7.1 Разработка RBD

При разработке структурной схемы надежности системы сначала необходимо дать определение состояниям успеха/отказа системы. Если используют несколько определений, то для каждого из них может потребоваться отдельная структурная схема надежности. Затем необходимо разделить систему на блоки, отражая логику их поведения в системе таким образом, чтобы каждый блок был статистически независимым и максимально большим. В то же время каждый блок, по возможности, не должен содержать резервирования.

На практике может потребоваться несколько попыток построения структурной схемы надежности (каждый раз повторяя описанные выше шаги) для того, чтобы получить подходящую RBD.

Следующий шаг относится к определению успеха/отказа системы и включает в себя построение линий, соединяющих блоки и формирующих путь успеха. На рисунках, приведенных ниже, показаны различные пути успеха от входа до выхода. Они объединяют такую комбинацию блоков, при функционировании которых система находится в работоспособном состоянии. Если для функционирования системы необходимо, чтобы функционировали все блоки, то в соответствующей структурной схеме надежности все блоки должны быть соединены последовательно, как показано на рисунке 1.

I — порт входа О — порт выхода, А, В, С, Z — блоки системы

Рисунок 1 — Последовательная структурная схема надежности

Структурные схемы такого типа называют последовательными или «последовательной моделью».

Если в соответствии с определением успеха/отказа системы отказ одного компонента или блока не влияет на функционирование системы, используют другой тип структурной схемы системы. Например, если вся последовательная цепочка дублирована, то структурная схема надежности системы имеет вид, показанный на рисунке 2. Если дублирован каждый блок последовательной цепочки, то структурная схема имеет вид, показанный на рисунке 3. Структурные схемы такого вида называют параллельными или «параллельной моделью». Следует помнить, что термины «дублированный», «резервированный» и «параллельный» близки по значению и далее используются как синонимы.

Рисунок 2 — Последовательно-параллельная структурная схема надежности

Рисунок 3 — Параллельно-последовательная структурная схема надежности

Структурные схемы надежности, используемые для моделирования безотказности системы, обычно представляют собой сложные комбинации последовательных и параллельных схем. Такую схему используют, если, например, надо учесть соединение трех блоков А, В и С и общего блока электропитания (D). В этом случае схема имеет вид, показанный на рисунке 4 или 5.

Рисунок 4 — Комбинированная структурная схема надежности с резервированием, вариант 1

Рисунок 5 — Комбинированная структурная схема надежности с резервированием, вариант 2

Для обеспечения статистической независимости отказ любого блока не должен вызывать изменение вероятности появления отказа любого другого блока системы. В частности отказ резервированного блока не должен влиять на блок электропитания системы или источник сигнала.

Часто возникает необходимость моделирования системы, определение успеха которой устанавливает, что для функционирования системы необходимо функционирование т или большего количества параллельных элементов. Структурная схема надежности такой системы принимает вид, показанный на рисунках 6 или 7.

Таким образом, для системы, изображенной на рисунке 6, отказ одного элемента является допустимым, а отказ двух или более приводит к отказу системы.

Большинство структурных схем надежности являются понятными, а условия успеха системы — очевидными. Однако не все структурные схемы могут быть сведены к комбинациям последовательных или параллельных систем. Пример такой структурной схемы надежности показан на рисунке 8.

Для успеха системы необходимо, чтобы в работоспособном состоянии были элементы В1 и С1 или элементы А и С1, или А и С2, или В2 и С2.

Рисунок 8 — Структурная схема надежности с последовательным и параллельным соединением блоков

Схема, изображенная на рисунке 8, может представлять собой схему системы подачи топлива на двигатели легкого самолета. Элемент В1 представляет собой поставку на двигатель левого борта (С1), элемент В2 — поставку на двигатель правого борта (С2), а элемент А — резервную поставку на оба двигателя. Для отказа данной системы необходимо, чтобы отказали оба двигателя.

Необходимо отметить, что во всех схемах, приведенных на рисунках 1-8 нет блоков, появляющихся на диаграмме несколько раз. Процедуры построения формул для оценки вероятности безотказности и работы систем этого типа приведены в разделе .

7.2 Оценка вероятности безотказной работы

Вероятность безотказной работы системы R_S(t) — это вероятность того, что система может выполнять требуемую функцию в установленных условиях в течение заданного интервала времени (0, t). В общем случае для вероятности безотказной работы справедлива формула

где λ(u) — интенсивность отказов системы в момент времени t = u.

Далее R_S(t) будет обозначаться R_S. Вероятность отказа системы F_S связана с вероятностью безотказной работы системы следующей зависимостью

F_s = 1 – R_S.

7.2.1 Последовательные модели

Для систем, RBD которых изображена на рисунке 1, зависимость вероятности безотказной работы системы R_S от вероятностей безотказной работы элементов описывает формула

т.е. вероятность безотказной работы системы равна произведению вероятностей безотказной работы всех блоков, входящих в систему.

Рисунок 9 — Структурная схема надежности системы с параллельным соединением блоков

7.2.2 Параллельные модели

Для систем, структурная схема надежности которых изображена на рисунке 9, зависимость вероятности отказа системы F_s от вероятностей отказа элементов описывает формула

F_S = F_A F_B.

Следовательно, для вероятности безотказной работы системы R_S справедлива формула

Формулы (1) и (2) могут быть объединены. Таким образом, если системе соответствует RBD, изображенная на рисунке 2, но с тремя блоками в каждой ветви, то для вероятности безотказной работы системы справедлива формула

Аналогично для вероятности безотказной работы системы, структурная схема надежности которой изображена на рисунке 3, справедлива формула

В общем случае для вероятности безотказной работы последовательной системы из n элементов справедливо выражение

Для RBD, изображенных на рисунках 4 и 5, формулы, связывающие R_S с вероятностями безотказной работы элементов, получают умножением выражений (3) и (4) на R_D.

7.2.3 Модели m из n (идентичные элементы)

Для вероятности безотказной работы системы, RBD которых изображены на рисунках 6 и 7, описывающие зависимость от вероятностей безотказной работы элементов, немного сложнее. Если система может быть представлена параллельным соединением n идентичных элементов, а для того, чтобы она была работоспособной, необходимо, чтобы были работоспособными не менее m элементов из n, то для вероятности безотказной работы системы справедливо выражение

Таким образом, вероятность безотказной работы системы, структурная схема надежности которой изображена на рисунке 6, имеет вид

где R — вероятность безотказной работы элемента.

Аналогично вероятность безотказной работы системы, структурная схема надежности которой приведена на рисунке 7, имеет вид

Для случая, когда m = (n — 1), R_s = nR^m — mRⁿ.

Если не все n элементов идентичны, рекомендуется использовать более общую процедуру (см. ).

7.2.4 Модели с ненагруженным резервом

Другой достаточно часто используемой формой резервирования является ненагруженный резерв (резервирование замещением) (см. ). Структурная схема надежности простой системы с ненагруженным резервом изображена на рисунке 10.

Рисунок 10 — Структурная схема надежности системы с ненагруженным резервом
(резервирование замещением)

На рисунке 10 блок А является активным элементом, а блок В находится в стадии ожидания и включается для замены элемента А в случае его отказа. Надежность устройств переключения и датчиков на рисунке 10 не рассматривается.

Формула, описывающая связь вероятности безотказной работы R(t) такой системы с вероятностью безотказной работы элементов, может быть получена после рассмотрения событий, которые могут произойти в течение заданной наработки t. Этими событиями могут быть следующие:

a) элемент А работоспособен в течение времени t;

b) элемент А с интенсивностью отказов λ_А и плотностью распределения f_A(τ), τ < t в начальный момент времени работоспособен и отказывает в момент времени τ < t

— элемент В (интенсивность отказов λ_Bd) в начальный момент времени находится в ненагруженном резерве (бездействует либо без нагрузки, либо со слабой нагрузкой);

— элемент В находится в состоянии ожидания отказа элемента А (время τ): в момент отказа элемента А элемент В переходит в активное состояние (интенсивность отказов λ_B) с помощью переключателя S (вероятность безотказной работы R_sw(τ)) и заменяет элемент А;

— элемент В сохраняет работоспособное состояние в течение оставшегося времени с вероятностью R_B(t — τ).

С учетом возможных событий вероятности безотказной работы системы соответствует формула

Если все элементы имеют постоянную интенсивность отказов в активном или пассивном состоянии, то приведенную формулу можно упростить

Примечание — Если вероятность безотказной работы переключателя не зависит от времени, но является функцией другой переменной (например, количества включений нагрузки и т.д.), рекомендуется не использовать эту функциональную зависимость, а учитывать вероятность безотказной работы переключателя, обозначая ее R_SW.

В этом случае приведенная формула имеет вид

В предположении об идеальном переключении λ_SW = 0 выражение принимает вид

Если интенсивность отказов элемента В в пассивном состоянии принять равной нулю, то формула для вероятности безотказной работы системы, резервированной замещением, будет иметь следующий вид

Если к тому же обе интенсивности отказов равны (λ_А = λ и λ_в = λ), то формула для вероятности безотказной работы системы будет иметь следующий вид

R_S(t) = e^—λt (1 + λt)

Если в таких идеальных условиях имеется не один, а n резервных элементов, формула для вероятности безотказной работы системы будет иметь следующий вид

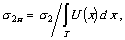
Примечание — Структурная схема надежности системы должна включать в себя блоки, характеризующие работоспособность устройств переключения и датчиков, которые часто являются слабым звеном системы.

Необходимо отметить, что в отличие от всех примеров, рассмотренных в настоящем стандарте, здесь вероятность безотказной работы элемента В зависит от времени, когда откажет элемент А. В этом случае отказы элементов А и В не могут считаться независимыми и поэтому для анализа системы необходимо использовать другие процедуры, например Марковский анализ.

8 Более сложные модели

8.1 Общие процедуры

8.1.1 Основные положения

Вероятность безотказной работы R_S(t) всех систем, рассмотренных выше, можно оценить с помощью соответствующей формулы, полученной на основе формул () — (). Однако существуют системы, вероятности безотказной работы которых невозможно оценить ни по одной из вышеуказанных формул. Эти системы являются более сложными и для них необходимо использовать другие методы анализа надежности. Для систем со сложной RBD обычно используют метод моделирования Монте-Карло (в настоящем стандарте он не рассматривается).

Стандарт распространяется на методы, в основе которых лежит предположение о независимости отказов в соответствии с .

8.1.2 Использование формулы полной вероятности

Для работы с RBD, аналогичной изображенной на рисунке 8, используют другие методы.

Один из возможных методов основан на формуле полной вероятности, которая может быть получена следующим образом.

Для n взаимно исключающих событий A₁,…,A_n сумма вероятностей которых равна единице, Р(В) = Р(В|А₁) Р(А₁) + … + Р(В|А_n) Р(А_n), где В — произвольное событие; Р(А_i) — вероятность появления события A_i; Р(В|А_i) — условная вероятность появления события В при условии появления события А_i.

Один из методов, используемых для анализа RBD систем, сводится к многократному применению следующего соотношения

R_S = P(SS)|X_{работоспособный}) P(X_{работоспособный}) + P(SS)|X_{отказавший}),

где R_S — вероятность безотказной работы системы;

P(SS)|X_{работоспособный}) — вероятность безотказной работы системы (вероятность успеха системы) при условии, что элемент X работоспособен;

P(SS)|X_{отказавший}) — вероятность безотказной системы при условии, что элемент X отказал.

Например, если в системе, RBD которой изображена на рисунке 8, элемент А отказал, структурная схема надежности системы принимает вид, изображенный на рисунке 11.

Рисунок 11 — Структурная схема надежности, изображенная на рисунке 8,
в случае отказа элемента А

P(SS)|A_{отказавший}) = R_B1 R_C1 + R_B2 R_C2 — R_B1 R_C1 R_B2 R_C2

Если элемент А работоспособен, структурная схема надежности, изображенная на рисунке 8, принимает вид, приведенный на рисунке 12.

Рисунок 12 — RBD, изображенная на рисунке 8,
в случае работоспособности элемента А

Таким образом

P(SS)|A_{работоспособный}) = R_C1 + R_C2 — R_C1 R_C2,

Следовательно

R_S = (R_C1 + R_C2 – R_C1 R_C2) R_A + (R_B1 R_C1 + R_B2 R_C2 – R_B1 R_C1 R_B2 R_C2) (1 — R_A).

Если R_C1 = R_C2 = R_C и R_B1 = R_B2 = R_B, вид выражения упрощается

Для проверки выражений () и () может быть применен метод, описанный в 8.1.2.

8.1.3 Использование таблиц истинности

Пути работоспособности (успеха) системы, изображенные с помощью схемы RBD, могут быть описаны булевыми выражениями. Например системе, состоящей из элементов А, В и С, соединенных параллельно (для того чтобы система была работоспособной достаточно одного работоспособного элемента), соответствует RBD, изображенная на рисунке 13.

Рисунок 13 — Параллельное соединение «один из трех»

Работоспособное состояние системы описывает булево выражение

где SS — событие, состоящее в том, что система находится в работоспособном состоянии, А, В и С — события, состоящие в том, что элементы А, В и С находятся в работоспособном состоянии.

Однако события А, В и С не могут быть непосредственно заменены в выражении (9) соответствующими вероятностями R_A, R_B, R_C для определения вероятности безотказной работы системы, потому что выражение (9) представляет собой последовательность объединений (дизъюнкций) пересекающихся событий (см. ). Выражение (9) можно записать как сумму непересекающихся событий следующим образом

С позиций булевой алгебры выражения (9) и (10) эквивалентны. Однако в выражении (10) каждое событие SS, А, , В, , С,  может быть заменено соответствующей вероятностью безотказной работы

R_S, R_A, (1 – R_A), R_B, (1 — R_B), R_C, (1 — R_C).

Таким образом

Существует также другой простой способ записи выражения (9) с помощью непересекающихся событий

Следовательно

Выражения (11) и (13) идентичны.

Процесс вывода формулы (11) может быть упрощен за счет применения таблицы истинности (таблица 1), позволяющей облегчить преобразование выражения (9) в выражение (10).

Просматривая таблицу 1 сверху вниз, можно записать следующие выражения, соответствующие работоспособному состоянию системы

Объединение этих записей с помощью логического «ИЛИ» приводит к выражению (10).

Все возможные комбинации (всего 32) работоспособного состояния и отказа элементов системы, структурная схема надежности которой изображена на рисунке 8, приведены в таблице 2.

С помощью таблицы 2 можно записать комбинации, соответствующие работоспособному состоянию системы, используя противоположные события

На основе формулы (14) легко вывести формулу, связывающую вероятность безотказной работы системы с вероятностями безотказной работы ее элементов

R_S = (1 — R_B1) (1 — R_B2) (1 — R_C1) R_C2 R_A + (1 — R_B1) (1 — R_B2) R_C1 (1 — R_C2) R_A +…

+ R_B1 R_B2 R_C1 R_C2 R_A.

Таблица 1 — Таблица истинности для примера, изображенного на рисунке 13

Таблица 2 — Таблица истинности для примера, изображенного на рисунке 8

Выражение () представляет собой объединение девятнадцати членов, описывающих комбинации работоспособного и неработоспособного состояния элементов, приводящие к успеху системы. Очевидно, что булевы таблицы истинности с увеличением количества элементов быстро становятся громоздкими и необозримыми, хотя принцип работы с ними очень прост. Детальное описание булевых методов приведено в .

8.2 Модели с общими блоками

В разделе все блоки входят в RBD только один раз. Это удобно при построении структурных схем вида, показанного на рисунке 14. Например, блоки С и D могут быть функционально подобными и представлять собой дублирующие друг друга элементы: элемент А подает питание только на элемент С, а элемент В может подавать питание на элементы С и D. На рисунке 14 представлено не только расположение элементов, но и структурная схема надежности. В такой структурной схеме надежности системы важно направление стрелок.

Рисунок 14 — Структурная схема надежности системы со стрелкой

Альтернативные пути успеха системы в вышеупомянутом примере могут быть представлены структурной схемой надежности, в которой некоторые блоки появляются несколько раз, как изображено на рисунке 15. В основе этой схемы лежит схема, изображенная на рисунке 14, после ее анализа и выделения пар элементов, одновременный отказ которых приводит к отказу системы. Таким образом, схема, представленная на рисунке 15, представляет собой последовательную комбинацию таких пар элементов.

Рисунок 15 — Альтернативное представление RBD, изображенной на рисунке 14, с использованием параллельных блоков

При работе с данной структурной схемой надежности неправильно рассматривать блоки, объединенные в пару как независимые, и затем определять вероятность безотказной работы системы. В этом случае необходимо использовать любой из методов, приведенных в и . Например, в соответствии с методом, описанным в 8.1.2:

R_S = P(SS)|B_{работоспособный}) P(B_{работоспособный}) + P(SS)|B_{отказавший}) P(B_{отказавший}),

где вероятность P(SS)|B_{работоспособный}) устанавливают в соответствии со структурной схемой надежности, включающей в себя параллельные блоки С и D. Поскольку

P(SS)|B_{отказавший}) = P(SS|(B_{отказавший}|C_{работоспособный}) P|C_{работоспособный}) +

+ P(SS)|B_{отказавший}|C_{отказавший})P(C_{отказавший}) = R_A R_C + 0.

Следовательно

R_S = (R_D + R_C — R_DR_C) R_B + R_AR_C (1 — R_B),

т.е. R_S = R_AR_C + R_BR_C + R_BR_D — R_AR_BR_C — R_DR_BR_C.

На рисунках 14 и 15 показаны различные способы моделирования отказа системы. А именно, отказ системы возникает тогда, когда отказали блоки А и В или В и С или С и D. Другими словами, булевы выражения для успеха (SS) или отказа (SF) системы, изображенной на рисунках 14 и 15, будут одинаковыми:

SS = A Ç B È B Ç C È B Ç D;

Применяя метод, описанный в , можно составить таблицу 3.

Таблица 3 — Таблица истинности для систем, изображенных на рисунках 14 и 15

Окончание таблицы 3

В соответствии с таблицей 3 можно вывести следующее выражение для описания вероятности безотказной работы системы R_S как функции вероятностей безотказной работы элементов

R_S = R_AR_BR_CR_D + R_AR_BR_C (1 — R_D) + R_AR_B(1 — R_C) R_D +

+ R_A (1 — R_B) R_C (1 — R_D) + (1 — R_A) R_BR_CR_D + (1 — R_A) R_BR_C (1 — R_D) + (1 — R_A) R_B (1 — R_C) R_D.

Это выражение можно упростить до следующего вида

R_S = R_AR_C + R_BR_D + R_BR_C — R_AR_BR_C — R_DR_BR_C

Еще один метод работы с общими блоками состоит в следующем. Сначала игнорируют то, что некоторые блоки входят в структурную схему надежности системы несколько раз и записывают выражение для вероятности безотказной работы системы R_S обычным способом:

R_S = (R_A + R_B — R_AR_B) (R_B + R_C — R_BR_C) (R_C + R_D — R_CR_D).

Если скобки перемножить (получив выражение в виде суммы 27 членов) и такие слагаемые как R_AR_BR²_C и R_dR_bR²_C заменить на их булевы эквиваленты R_AR_BR_C и R_DR_BR_C соответственно, то выражение для вероятности безотказной работы системы R_S можно упростить до следующего вида

R_S = R_AR_C + R_BR_D + R_BR_C — R_AR_B R_C — R_DR_BR_C

8.3 Модели m из n (неидентичные элементы)

Метод, описанный в , в данном случае не применим. Как пример рассмотрим структурную схему надежности, представленную на рисунке 16.

Рисунок 16 — Система 2 из 5 (неидентичные элементы)

Для оценки вероятности безотказной работы такой системы можно использовать методы, описанные в или . В соответствии с методом, описанным в для вероятности отказа системы F_s, справедливо следующее выражение

F_S = (1 — R_A) (1 — R_B) (1 — R_C) (1 — R_D) (1 – R_E) + (1 — R_A) (1 — R_B) (1 — R_C) (1 — R_D) R_E +

+ (1 — R_A) (1 — R_B) (1 — R_C) R_D (1 – R_E) + (1 — R_A) (1 — R_B) R_C(1 — R_D) (1 – R_E) +

+ (1 — R_A) R_B (1 — R_C) (1 — R_D) (1 – R_E) + R_A (1 — R_B) (1 — R_C) (1 — R_D) (1 – R_E).

Вероятность безотказной работы системы R_S определяют по формуле

R_S = 1 — F_S.

Примечание — Более эффективные методы для данного случая описаны в приложении В.

8.4 Метод редукции

Иногда структурные схемы надежности выглядят очень сложными. Однако предварительный ана­лиз, как правило, позволяет сгруппировать отдельные элементы в статистически независимые блоки. Это означает, что в данной системе нет групп, содержащих одинаково обозначенные блоки.

Например рассмотрим структурную схему надежности, изображенную на рисунке 17.

Рисунок 17 — Структурная схема надежности с группировкой элементов в блоки для редукции

Эту структурную схему можно упростить до схемы, изображенной на рисунке 18 а, путем группировки элементов в четырех блоках Х1, Х2, Х3 и Х4, обведенных пунктирной линией, и оценки вероятности безотказной работы этих блоков в соответствии с , , и .

Структурная схема надежности, изображенная на рисунке 18 а, может быть далее упрощена до RBD, изображенной на рисунке 18 b.

Рисунок 18 — Упрощенные структурные схемы надежности

Следовательно, формула для вероятности безотказной работы системы, соответствующая структурной схеме надежности, изображенной на рисунке 18 b), будет иметь вид (см. 7.2.2)

R_S = R_X1R_X2 + R_X3R_X4 – R_X1R_X2R_X3R_X4.

9 Применение метода для вычисления
коэффициента технического использования

В некоторых случаях все формулы и методы, приведенные в настоящем стандарте, могут быть применены для вычисления коэффициента технического использования. Для этого необходимо заменить обозначения вероятности безотказной работы на соответствующие обозначения коэффициента технического использования.

Применение методов правомерно только в том случае, если отказы и ремонт элементов не зависят друг от друга. На практике это означает, что отказ одного элемента не влияет на возникновение отказа другого элемента и имеется доступный бесконечный парк запасных частей и служб ремонта.

Другими словами, среднее время простоя любого элемента должно быть характеристикой только этого элемента и не должно зависеть от того, сколько других элементов отказало и нуждается в ремонте. На практике это означает, что основное внимание следует уделять схеме соединения элементов и тщательно проверять, является ли каждый элемент легко доступным для ремонта и не влияет ли его состояние на другие элементы.

Приложение А
(справочное)
Расчетные формулы

В таблице, приведенной в настоящем приложении, использованы термины «нагруженный резерв» и «ненагруженный резерв». Термин «нагруженный резерв» использован для указания того, что соответствующие блоки (каждый из которых может состоять из элементов подсистем, систем и т.д.) находятся под нагрузкой (включены) и, следовательно, могут отказать. Термин «ненагруженный резерв» использован для указания того, что блок или блоки не находятся под нагрузкой (выключены) и таким образом не могут отказать.

Таблица

Окончание таблицы

Приложение В
(справочное)
Булевы методы

B.1 Вводные замечания

Кроме булевых таблиц истинности, описанных в , при анализе RBD главным образом используют обычные математические формулы. Однако для анализа RBD может применяться также булева алгебра. Во многих случаях это является намного более эффективным. В частности булева алгебра может применяться в тех случаях, когда:

a) RBD содержит общие блоки (см. рисунок );

b) RBD содержит стрелки (см. рисунки и );

c) система очень сложная;

d) легче построить булево выражение для описания успеха (или отказа) системы, чем соответствующую RBD.

В отношении случая, указанного в перечислении d), следует заметить следующее. Для многих систем описание успеха или отказа с помощью булевой алгебры часто является более простой и понятной задачей, чем построение RBD. Использование булевого метода при анализе надежности системы позволяет избежать ошибок в процессе построения RBD.

B.2 Обозначения

Символы È и Ç ранее использовались для обозначения логических «ИЛИ» и «И» соответственно. Однако более удобно использовать символ «+» для обозначения логического «ИЛИ» и точки «.» для обозначения логического «И»¹⁾. Черточка над логической переменной обозначает инверсию или дополнение соответствующего события, например,  обозначает «не а». Выражение (a.b..e + f.g) следует читать как «а И b И НЕ с И е ИЛИ f И g». Текст, в котором используют символы, должен четко описывать их значение.

B.3 Логические переменные и вероятности

Рассмотрим систему из двух резервированных элементов, изображенную на рисунке 9. Очевидно, что система будет работоспособна, если будет работоспособен один из блоков А или В.

Булево выражение для успеха (работоспособного состояния) системы имеет вид

где а и b — логические переменные, соответствующие работоспособному состоянию блоков А и В соответственно. Если заменить а и b на R_a и R_b соответственно, формула (15) примет вид

К сожалению формула (16) является некорректной для зависимых событий. Если формулу (15) записать в виде

то замена а на R_a,  на (1 — R_a) и b на R_b, позволяет вывести корректную формулу для вероятности безотказной работы системы R_S

Процесс замены формулы (15) на формулу (17) называют ее представлением в виде непересекающихся (независимых) событий. Формулу (15) можно записать в другой форме: . При замене b на R_b и  на (1 — R_b) получаем корректную формулу вероятности безотказной работы системы (R_S)

Очевидно, что уравнения (18) и (19) эквивалентны.

¹⁾ Преимущества такой замены становятся очевидными в выражениях вида

Запись этого выражения с использованием логических символов имеет вид

Это выражение является более сложным для анализа.

Таким образом, основной целью является составление булева выражения для описания успеха системы с помощью непересекающихся событий. Это означает, что каждый член заключительного булева выражения для успеха системы должен быть независимым по отношению к каждому другому члену этого выражения.

В.4 Метод составления булевых выражений

B.4.1 Основные положения

Два члена являются взаимно непересекающимися (дизъюнктными), если, по крайней мере, одна переменная первого члена появляется в виде ее дополнения в другом члене. Например члены (каждый содержит по четыре логических переменных) p.q.r.s и t.u.v. являются непересекающимися за счет переменной s. Обратное также верно. В то же время два члена не являются непересекающимися (т.е. являются пересекающимися), если ни одна из переменных одного члена не появляется в другом в виде ее дополнения. Например два члена p.q.r.s и s.t.u.v не являются пересекающимися.

B.4.2 Принцип дизъюнкции

Если два члена T₁ и T₂ не являются непересекающимися и необходимо сделать T₂ независимым от T₁, то сначала необходимо выбрать все переменные в T₁ которые не входят в T₂. Такой член называют относительным дополнением T₂ до T₁. Предположим, что относительное дополнение — это (v₁.v₂.v₃.v₄). Тогда при замене Т₂ и T^*₂

выражение (T₁ + Т^*₂) будет состоять только из непересекающихся членов

Например, чтобы сделать член T₂ = d.e.f непересекающимся с членом Т₁ = a.b.c.d.e, необходимо выполнить следующие действия:

Относительным дополнением Т₂ до T₁ является пересечение а.b.с, поэтому если Т₂ (Т = d.e.f) заменить на T^*₂:

то T₁ и Т^*₂ (т.е. все члены a.b.c.d.e, d.e.f, a.d.e.f, a.b.d.e.f) будут непересекающимися (независимыми) относительно друг друга.

Примечание — Несмотря на то, что можно записать данное выражение для T^*₂ в виде

такая форма не подходит для процедуры, описанной в В.4.3.

В.4.3 Процедура перехода к независимым событиям

Процедура перехода к независимым событиям состоит в следующем.

a) Записывают выражение для успеха системы (обозначаемого SS₁), используя все члены булева выражения и обозначая их слева направо¹⁾ «T₁₁, T₁₂, T₁₃, …».

b) Выделяют T₁₁ как «основной» член и сравнивают T₁₁ с T₁₂.

c) При необходимости (т.е. если два члена являются пересекающимися), делают T₁₂ непересекающимся с T₁₁ в соответствии с В.4.2.

d) При необходимости делают T₁₃ непересекающимся с T₁₁.

e) Продолжают процесс для оставшихся членов выражения SS₁.

f) Проверяют несколько расширенное (из-за дополнительно добавленных членов) полученное на этом этапе выражение и упрощают его (по возможности), используя правила булевой алгебры (обычно применяют правила (х + х) = х, (х + х.у) = х, (х.у + у) = у). Полученное в результате выражение обозначают SS₂, а его члены слева направо обозначают «T₂₁, T₂₂, T₂₃, …».

g) Выбирают в качестве «основного» второй член SS₂ (T₂₂), сравнивают T₂₂ с T₂₃ и выполняют действия, описанные в перечислениях с) — f) для SS₂. Полученное в результате выражение обозначают SS₃.

h) Продолжают выполнять описанную процедуру до тех пор, пока все члены не будут использованы в качестве «основных». Таким образом, в полученное выражение будут входить только непересекающиеся члены. Полученное выражение представляет собой дизъюнктную версию исходного выражения SS₁. Если в таком булевом выражении для успеха системы каждую логическую переменную заменить соответствующей вероятностью безотказности работы, то будет получена формула для определения вероятности безотказной работы системы. При подстановке в это выражение числовых значений можно получить числовое значение вероятности безотказной работы системы.

Пример применения данной процедуры приведен в подразделе В.6.

¹⁾ Простые булевы выражения для успеха системы представляют собой произведение одного, двух или более членов.

B.5 Комментарии

Самое важное свойство метода состоит в том, что на основе последовательности шагов может быть составлена компьютерная программа. Использование современных компьютеров позволяет почти мгновенно получить формулы для достаточно сложных булевых выражений.

Другим достоинством метода является то, что описанная процедура может быть применена к булевым выражениям, полученным в результате исследования дерева неисправностей.

Еще одно важное свойство связано с тем, что полученное выражение используют для вычисления вероятностей, а также коэффициента технического использования. В этом случае каждое событие должно быть независимым от других. Это означает, что отказ и ремонт любого элемента не влияют на отказ или ремонт любого другого элемента (см. также раздел 9).

B.6 Пример применения дизъюнктирующей процедуры

Предположим, что система состоит из пяти элементов А, В, С, D и Е. Обозначим их соответствующими булевыми переменными а, b, с, d, е. Предположим, что успех системы в терминах булевой алгебры (SS) описывает выражение, включающее в себя четыре члена:

SS = a.b + e.b + e.d + c.d.

Для получения выражения с непересекающимися членами необходимо выполнить следующие действия.

Шаг 1.1. Каждый член делают непересекающимся с первым. Выполняют процедуру для получения второго члена, не пересекающегося с первым. Анализируют на наличие в первом члене дополнений переменных второго члена. Если это выполняется, то два члена являются непересекающимися, поэтому дальнейших действий не требуется. В противном случае необходимо выбрать все переменные первого члена (a.b), которые не появляются во втором члене (e.b). В терминах булевой алгебры это называется относительным дополнением второго члена до первого. В данном примере результатом является переменная а.

Шаг 1.2. Заменяют второй член (e.b), на ()¹⁾.

Шаг 1.3. Формируют третий член, не пересекающийся с первым. Анализируют первый и третий члены на наличие дополнения переменных первого члена в третьем члене. Так как это не выполняется, идентифицируют относительное дополнение третьего члена до первого. Это переменные а и b. Следовательно, необходимо заменить третий член на член ( + ).

Шаг 1.4. Формируют четвертый член (c.d), не пересекающийся с первым. Относительное дополнение четвертого члена до первого — переменные а и b.

Поэтому заменяют четвертый член на ( + ).). Таким образом, выражение для успеха системы на данном этапе принимает вид

Затем повторяют процесс, начиная co второго члена (этап 2).

Шаг 2.1. Формируют третий член SS₁ (), не пересекающийся со вторым (). Относительным дополнением является b. Заменяют ()) на ().

Шаг 2.2. Формируют четвертый член SS₁ (), не пересекающийся со вторым (). В этом случае члены уже являются непересекающимися (из-за переменных а и b), поэтому дальнейших действий не требуется.

Шаг 2.3. Формируют пятый член SS₁ (), не пересекающийся со вторым (). Относительным дополнением являются переменные е и b. Заменяют пятый член на ().

Шаг 2.4. Формируют шестой член SS₁ не пересекающийся со вторым. В этом случае члены уже являются непересекающимися (из-за переменной b), поэтому дальнейших действий не требуется.

Таким образом, выражение успеха системы на данном этапе принимает вид

На этой фазе третий член «поглощает» шестой, а третий и четвертый члены объединяются и дают (b.e.d). Другими словами

Таким образом, SS₂ имеет вид

Затем повторяют процесс, начиная с третьего члена (этап 3).

Шаг 3.1 Формируют четвертый член SS₂ (), не пересекающийся с третьим ()). В данном случае эти члены уже являются непересекающимися (из-за переменной е), поэтому дальнейших действий не требуется.

Шаг 3.2 Формируют пятый член SS₂, не пересекающийся с третьим. Относительным дополнением является переменная е. Таким образом, () заменяют на ().

¹⁾ Первый и второй члены теперь являются непересекающимися за счет переменной а. Она присутствует в первом члене, а во втором члене присутствует ее дополнение .

Выражение для успеха системы на данном этапе принимает вид

Так как дальнейшее упрощение невозможно, это выражение является искомым результатом. Заменяя переменные на соответствующие вероятности безотказной работы, получают выражение для вероятности безотказной работы системы

R_S = R_aR_b + (1 — R_a) R_eR_b + (1 – R_b) R_eR_d + (1 – R_e) (1 — R_a) R_cR_d + (1 – R_e) R_a (1 – R_b) R_cR_d.

Форма заключительного результата (в этом случае SS₃) зависит от порядка, в котором записаны члены в исходном булевом выражении. Например, если SS₁ имеет вид

SS^*₁ = c.d + e.d + e.b + a.b,

то итоговое выражение будет иметь вид

Хотя выражения для SS₃ и SS^*₃ выглядят очень разными, они эквивалентны.

Ключевые слова: система, элемент, структурная схема надежности, работоспособное состояние, отказ, последовательное соединение, параллельное соединение, булева алгебра, вероятность безотказной работы, интенсивность отказов, таблица истинности, нагруженный резерв, ненагруженный резерв, дизъюнкция