ГОСТ 25-101-83 Расчеты и испытания на прочность Методы схематизации случайных процессов нагружения элементов машин и конструкций и статистического представления результатов

Постановлением Государственного комитета СССР по стандартам от 12 июля 1983 г. № 3066 дата введения установлена

01.07.84

Ограничение срока действия снято по протоколу № 3-93 Межгосударственного совета по стандартизации, метрологии и сертификации (ИУС 5-6-93)

Настоящий стандарт устанавливает методы схематизации случайных процессов нагружения, возникающих в условиях эксплуатации или испытаний элементов машин и конструкций, и статистического представления результатов схематизации.

Результаты схематизации используют для:

расчетной оценки усталостной долговечности элементов по критериям накопления усталостных повреждений на стадиях до появления макроскопической усталостной трещины и ее развития;

сравнительной оценки процессов нагружения однотипных элементов с целью выявления наиболее нагруженных элементов;

количественной оценки эксплуатационных режимов машин и конструкций по их повреждающему воздействию;

моделирования реального нагружения элементов при испытаниях на усталость и расчетном определении характеристик их сопротивления усталости.

Настоящий стандарт не распространяется на методы вычисления корреляционных, автокорреляционных функций и спектральных плотностей процессов реального нагружения, а также методы выбора теоретического закона распределения и проверки согласия с эмпирическим распределением.

СОДЕРЖАНИЕ

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Объектом исследования является реализация случайного процесса нагружения элементов машин или конструкции (изменение во времени нормальных и касательных напряжений, сил, моментов, линейных и угловых деформаций и др.) x(t), далее — процесса нагружения.

1.2. Схематизация процессов нагружения элементов машин и конструкций и статистическое представление результатов схематизации включает следующие этапы:

предварительная подготовка процесса нагружения к схематизации;

дискретизация процесса нагружения (ГОСТ 23207-78);

вычисление статистических характеристик дискретной последовательности ординат процесса нагружения;

выделение экстремумов процесса по дискретной последовательности его ординат;

замена реального процесса нагружения схематизированным по выбранному методу схематизации;

получение эмпирических распределений нагрузок схематизированного процесса и вычисление основных статистических характеристик распределений.

Примечание. В зависимости от применяемых алгоритмов и технических средств допускается изменение последовательности и исключение этапов.

1.3. Схематизацию процессов нагружения проводят применительно к блоку нагружения (ГОСТ 23207-78), который соответствует совокупности последовательных значений переменных нагрузок, возникающих в элементе конструкции за какой-либо характерный период эксплуатации (один полет самолета, l_б километров пробега автомобиля по дороге определенного профиля, l_б часов работы и т.д.).

1.4. Длительность записи или длина реализации процесса нагружения, соответствующая блоку нагружения, должна содержать не менее 1000 экстремумов n_э процесса.

Примечание. Допускается проводить схематизацию для коротких процессов с числом экстремумов менее 1000. В этом случае рекомендуется оценивать погрешность, вносимую использованием недостаточно представительных по числу экстремумов реализаций.

1.5. При схематизации не учитывают колебания, амплитуда которых меньше половины ширины класса.

1.6. Термины и определения, применяемые в стандарте, соответствуют ГОСТ 23207-78, ГОСТ 21878-76. Условные обозначения приведены в .

1.7. Теоретические основы стандарта приведены в .

2. ПОДГОТОВКА, ДИСКРЕТИЗАЦИЯ И ОЦЕНКА СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПРОЦЕССА НАГРУЖЕНИЯ

2.1. Подготовка процесса нагружения к схематизации

2.1.1 Разбиение процесса нагружения на классы

Диапазон изменения нагрузок процесса

                                                                                   (1)

разбивается равноотстоящими уровнями нагрузок на классы шириной

                                                                                                   (2)

Величина Δ отражает масштаб при схематизации и показывает, какая нагрузка соответствует одному классу. Количество классов т должно удовлетворять неравенству

14 ≤ m ≤ 32.

Нумерация классов i производится снизу вверх в направлении возрастания нагрузок процесса, начиная с первого класса в области X_min. Пример разбиения на классы показан на черт. 1.

Разбиение на классы

Черт. 1

Класс, в который попадает значение средней нагрузки , называется классом средней нагрузки и обозначается . Класс, в котором располагается значение нагрузки, равное нулю, обозначается i₀

Если величина нагрузки попадает на границу класса, то ее следует относить к классу с большим номером.

2.1.2. Определение максимальной частоты процесса F_max

Для определения F_max разбивают процесс на 20-50 равных фрагментов длительностью t_ф, измеряемой в секундах. В каждом фрагменте подсчитывают количество экстремумов. Соседние экстремумы, образующие размах меньше ширины класса, не подсчитывают. Значение F_max определяют по формуле

,                                                                                               (3)

где n_э — максимальное для рассмотренных фрагментов число экстремумов.

2.1.3. Определение минимальной длины процесса нагружения

Минимальную длину процесса нагружения, необходимую для схематизации, выбирают с учетом , что обеспечивает достаточную статистическую представительность результатов.

Примечание. Допускается выбирать из общей длины процесса нагружения несколько отдельно взятых участков, соответствующих каждому режиму нагружения, входящему в блок нагружения, при условии выполнения для каждого участка (например, запись процесса нагружения элементов самолета за один полет может быть представлена участками руления, взлета, горизонтального полета и посадки).

2.2. Дискретизация процесса нагружения

Проведению схематизации предшествует дискретное представление процесса нагружения в виде последовательности ординат процесса для ввода цифровой информации в ЭВМ и вычисления статистических характеристик.

Дискретизация может осуществляться методом случайных ординат или методом пересечений.

2.2.1. Дискретизация по методу случайных ординат

На черт. 2 показана дискретизация по методу случайных ординат. Значения процесса нагружения x(t) определяют через равные промежутки времени Δt, в результате получают случайную последовательность ординат процесса нагружения.

Дискретизация по методу случайных ординат

Черт. 2

Интервал дискретизации Δt определяют по формуле

.                                                                                     (4)

2.2.2. Дискретизация по методу пересечений

При дискретизации по методу пересечений ординаты процесса нагружения определяют в момент пересечения верхней границы класса восходящей или нисходящей ветвями процесса. На черт. 3 иллюстрируется дискретизация по восходящим ветвям процесса.

Примечание. Допускается использовать метод пересечений для схематизации процесса нагружения ().

Дискретизация по методу пересечений

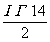
Черт. 3

2.3. Оценка статистических характеристик процесса нагружения

Для выбора метода схематизации, ее проведения и общей характеристики процесса нагружения вычисляют ряд статистических характеристик по последовательности ординат процесса: среднеарифметическое значение процесса нагружения (средняя нагрузка) , вычисляют как выборочное среднее;

дисперсию процесса нагружения S², вычисляют как выборочную дисперсию;

среднеквадратическое отклонение процесса нагружения S, вычисляют как выборочное среднеквадратическое отклонение;

коэффициент нерегулярности процесса нагружения к вычисляют согласно ГОСТ 23207-78) по формуле

,                                                                                  (5)

 

где n₀ — число пересечений процессом уровня средней нагрузки;

n_э — число экстремумов того же процесса.

3. МЕТОДЫ СХЕМАТИЗАЦИИ ПРОЦЕССОВ НАГРУЖЕНИЯ

Методы схематизации устанавливают правила выделения цикла или полуцикла регулярного нагружения из исследуемого процесса нагружения.

Полуцикл нагружения составляет часть цикла регулярного нагружения (ГОСТ 23207-78), которая соответствует половине периода изменения нагрузки.

Схематизированная реализация случайного процесса нагружения (ГОСТ 23207-78), далее — схематизированный процесс, представляет собой совокупность выделенных по одному из методов схематизации циклов или полуциклов нагружения.

Последовательность нагрузок  в схематизированном процессе может быть представлена:

при однопараметрической схематизации — последовательностью амплитуд  или размахов выделенных циклов a_j

при двухпараметрической схематизации — корреляционной таблицей (п. ) или последовательностью приведенных к симметричному циклу нагружения амплитуд x_прj Полученную по методу

схематизации последовательность нагрузок группируют по интервалам, образуя эмпирическое распределение частот повторения нагрузок схематизированного процесса h (x_s) ().

3.1. Выделение экстремумов

Непосредственно перед схематизацией по любому из методов должно проводиться выделение экстремумов. Соседние экстремумы, образующие размах меньше ширины класса, выделению не подлежат.

3.2. Однопараметрические методы схематизации

3.2.1. Метод экстремумов

По данному методу рассматривают все положительные максимумы и все отрицательные минимумы (ГОСТ 23207-78) процесса нагружения. На черт. 4 иллюстрируется выделение амплитуд по методу экстремумов. За амплитуды нагружения принимают модуль разности каждого из указанных экстремумов х_эj и медианой экстремумов процесса нагружения х₅₀ (ГОСТ 23207-78)

 = | х_эj — х₅₀|.                                                                     (6)

Схематизация по методу экстремумов

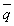
Черт. 4

По последовательности значений  определяют распределение частот повторения амплитуд полуциклов нагружения h(x_a).

3.2.2. Метод максимумов

По данному методу рассматривают все положительные максимумы. На черт. 5 иллюстрируется схематизация по методу максимумов. За амплитуды нагружения принимают разность

=— х₅₀.                                                                                         (7)

По последовательности значений  определяют распределение частот повторения амплитуд циклов h(x_a).

Схематизация по методу максимумов

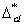
Черт. 5

3.2.3. Метод минимумов

По данному методу рассматривают все отрицательные минимумы. На черт. 6 иллюстрируется схематизация по методу минимумов. За амплитуду принимают разность

= х₅₀ — .                                                                 (8)

По последовательности значений  определяют распределение частот повторения амплитуд циклов h(х_а).

Схематизация по методу минимумов

Черт. 6

3.2.4. Однопараметрический метод размахов

На черт. 7 иллюстрируется схематизация по однопараметрическому методу размахов. За размах принимают абсолютное значение разности следующих друг за другом экстремумов

.                                                                 (9)

Схематизация по однопараметрическому методу размахов

Черт. 7

Учитывают размахи как на восходящих, так и на нисходящих ветвях процесса. Амплитуды полуцикла нагружения определяют как половину размаха

                                                                            (10)

Примечание. Допускается проводить схематизацию только по восходящим или по нисходящим ветвям процесса.

3.3. Двухпараметрические методы схематизации

При двухпараметрической схематизации результат представляют либо в виде корреляционной таблицы, либо в виде распределения приведенных амплитуд.

3.3.1. Двухпараметрический метод размахов

Схематизацию по этому методу проводят аналогично однопараметрическому методу размахов, однако учитывают не только величину размаха, но и положение размаха относительно нагрузки, равной нулю. На черт. 8 показана схематизация по двухпараметрическому методу размахов. В результате схематизации заполняют корреляционную таблицу (п. ). Схематизацию проводят по восходящим и нисходящим ветвям процесса нагружения.

Примечание. Допускается проводить схематизацию только по восходящим или по нисходящим ветвям процесса.

Схематизация по двухпараметрическому методу размахов

Черт. 8

3.3.2. Корреляционная таблица

Корреляционная таблица является одной из форм представления результата при двухпараметрической схематизации. В каждой ее клетке содержится накопленное число выделенных циклов или полуциклов нагружения. Величина интервала разбиения каждого параметра корреляционной таблицы равна или кратна ширине класса Δ.

Допускается использовать две формы корреляционной таблицы:

корреляционная таблица максимумов и минимумов (параметрами таблицы являются максимумы и минимумы выделенных циклов или полуциклов);

корреляционная таблица амплитуд и средних значений (параметрами таблицы являются амплитуда и среднее выделенных циклов или полуциклов).

При заполнении корреляционной таблицы указывают, построена она для циклов или для полуциклов.

3.3.2.1. Корреляционная таблица максимумов и минимумов.

Корреляционная таблица максимумов и минимумов показана в табл. 1. По вертикали сверху вниз и по горизонтали слева направо указывают номера классов.

Регистрацию j-го цикла (полуцикла) проводят в клетке корреляционной таблицы с координатами: по вертикали — номер класса ( ), в которой попадает максимум; по горизонтали — номер класса (), в который попадает минимум. Табл. 1 заполнена для полуциклов процесса нагружения, изображенного на черт. 8 при схематизации его по двухпараметрическому методу размахов. Так, например, полуцикл с размахом а₁ попадает в заштрихованную в табл. 1 клетку, поскольку  лежит в классе № 6, a  — в классе № 4. В данном примере ширина класса и интервала совпадает.

Таблица 1

Корреляционная таблица максимумов и минимумов

На основании корреляционной таблицы максимумов и минимумов могут быть получены три однопараметрических распределения:

суммирование содержимого клеток в таблице в направлении строк дает распределение минимумов h(x_min);

суммирование в направлении столбцов дает распределение максимумов h(х_mах);

суммирование в направлении диагоналей, указанных в табл. 1, дает распределение амплитуд h(х_а).

3.3.2.2. Корреляционная таблица амплитуд и средних значений.

Амплитуду  и среднее значение  для j-го цикла (полуцикла) в единицах класса определяют по формулам:

;                                                                                        (11)

.                                                                                        (12)

Регистрацию j-го цикла (полуцикла) проводят в клетке корреляционной таблицы с координатами: по вертикали  ; по горизонтали .

Корреляционная таблица амплитуд и средних значений показана в табл. 2. Табл. 2 заполнена для полуциклов процесса нагружения, изображенного на черт. 8 при схематизации его по двухпараметрическому методу размахов. Например, полуцикл с размахом a₁₀ попадает в заштрихованную клетку таблицы, поскольку амплитуда полуцикла  = 3,0, а среднее цикла  = 5,0.

На основании корреляционной таблицы амплитуда и средних значений могут быть получены два однопараметрических распределения:

суммирование по строкам таблицы дает распределение амплитуд h(x_a);

суммирование по столбцам таблицы дает распределение средних значений циклов (полуциклов) h(x_m).

Таблица 2

Корреляционная таблица амплитуд и средних значений

3.3.3. Методы выделения полных циклов

К методам выделения полных циклов относят:

метод полных циклов;

метод «дождя».

Оба метода приводят к практически одинаковым результатам.

Допускается применять методы выделения полных циклов и при однопараметрической схематизации.

3.3.3.1. Метод полных циклов

По данному методу осуществляют выделение циклов постепенно в несколько просмотров, начиная с циклов с наименьшим размахом. На черт. 9 приведена схематизация по методу полных циклов. Исходный процесс нагружения показан на черт. 9а. Здесь вначале выделяют заштрихованные циклы с размахом Δ ≤ а < 2Δ, которые регистрируют и из дальнейшего рассмотрения исключают. Процесс x₁(t)_, изображенный на черт. 9б, получен из исходного х (t) после исключения циклов с Δ ≤ а < 2Δ. Затем выделяют циклы с 2Δ ≤ a < 3Δ (черт. 9б). Процесс х₂(t), изображенный на черт. 9в, получен из процесса x₁(t) после исключения циклов с размахом 2Δ ≤ а < 3Δ. После исключения циклов с размахами а < 7Δ будет получен процесс x₃(t), изображенный на черт. 9г. Процесс х₃(t) представляет собой один цикл, образованный Х_mах и X_min с наибольшим размахом a_mах.

Схематизация по методу полных циклов

Черт. 9

3.3.3.2. Метод «дождя»

Схематизация по методу «дождя» приведена на черт. 10. При схематизации удобно представить, что ось времени направлена вертикально вниз. Пусть линии, соединяющие соседние экстремумы — это последовательность крыш, по которым стекают потоки дождя. Номерам максимумов соответствуют нечетные числа, номерам минимумов — четные.

Схематизация по методу «дождя»

Черт. 10

Траектории потоков определяют в соответствии со следующими правилами:

1. Потоки начинаются с внутренней стороны экстремумов последовательно. Каждый поток определяет полуцикл нагружения. Величину размаха определяют проекцией траектории потока на ось нагрузки.

2. Поток, начавшийся в точке максимума, прерывается в тот момент, когда встретится максимум больший, чем исходный. Например, поток из максимума 1 стекает по направлению к максимуму 2 и прерывается напротив максимума 3, поскольку он больше исходного.

3. Поток, начавшийся в точке минимума, прерывается, когда встретится минимум меньший, чем исходный. Например, поток из точки 10 прерывается напротив 16, поскольку минимум 16 меньше исходного.

4. При встрече на одной из крыш нескольких потоков движение продолжает тот, который берет начало в экстремуме с меньшим номером, а остальные прерываются. Например, поток из точки 5 продолжает свой путь, а потоки из точек 7 и 9 прерываются.

5. Поток, не встретивший препятствий, падает на землю, например поток из максимума 19.

Метод «дождя» позволяет ввести схематизацию в режиме реального времени. При этом запоминают лишь траектории потоков дождя и обработку проводят по мере ввода экстремумов.

3.4. Приведение асимметричных циклов нагружения к эквивалентным симметричным

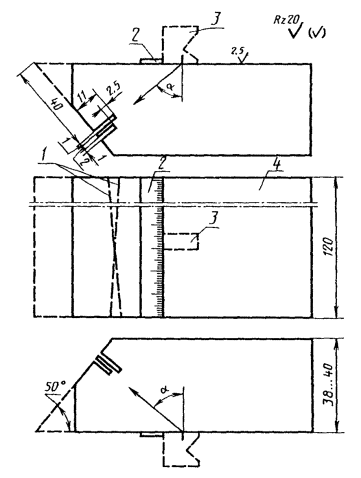
Для учета влияния асимметрии цикла нагружения при определении характеристик сопротивления усталости элементов машин и конструкций полученные в результате схематизации корреляционные таблицы преобразуют в однопараметрические таблицы распределения эквивалентных (в смысле вносимого усталостного повреждения) амплитуд. Приведение осуществляют по формуле

                                                             (13)

 

где φ — коэффициент чувствительности к асимметрии цикла нагружения.

Коэффициент чувствительности к асимметрии цикла нагружения для сталей выбирают по ГОСТ 25.504-82. Для других материалов значение коэффициента φ должно быть подтверждено экспериментально или теоретически.

В ряде случаев более удобным является получение однопараметрических распределений приведенных амплитуд по последовательности амплитуд и средних нагрузок каждого выделенного цикла нагружения  без использования корреляционных таблиц.

4. ВЫБОР МЕТОДА СХЕМАТИЗАЦИИ. КРИТЕРИИ ВЫБОРА

Каждый из методов схематизации, изложенных в , имеет свои особенности применения в зависимости от характера подлежащего схематизации процесса нагружения. Для обоснованного выбора метода схематизации в пп. 4.1-4.7 кратко изложены особенности каждого из них.

4.1. При использовании методов экстремумов, максимумов и минимумов (пп. ; ; ) не учитывают отрицательные максимумы и положительные минимумы. Это приводит к заниженному количеству зарегистрированных циклов нагружения по сравнению с количеством циклов, образуемым всеми максимумами и минимумами процесса. В целом схематизированный процесс по методу экстремумов будет более повреждающим, чем реальный, поскольку мелкие наложенные циклы нагружения учитывают с завышенной амплитудой, например амплитуда  процесса нагружения, изображенного на черт. 4.

4.2. Методы максимумов и минимумов дают удовлетворительные результаты для процессов с симметричным относительно средней нагрузки распределением экстремумов.

4.3. При использовании однопараметрического метода размахов (п. ) не учитывают средние значения каждого выделенного цикла. Поэтому метод может быть использован только для процессов с незначительным изменением среднего значения циклов нагружения или для оценки нагружения элементов машин и конструкций, сопротивление усталости материала которых зависит практически только от переменной составляющей цикла нагружения.

4.4. Методы размахов как однопараметрический, так и двухпараметрический (п. ) приводят к схематизированному процессу менее повреждающему, чем реальный, так как не учитывают циклы с большой амплитудой, на которые наложены мелкие циклы нагружения.

4.5. Методы выделения полных циклов (п. ) имеют преимущество по сравнению с перечисленными методами, поскольку учитывают как основные, так и наложенные циклы (см. ).

4.6. Все методы схематизации, изложенные в настоящем стандарте, в равной степени применимы к процессам нагружения с коэффициентом нерегулярности к = 1.

Для меньших значений к возрастает различие в результатах схематизации, полученных с применением разных методов.

4.7. Область применения методов схематизации, изложенных в , для процессов нагружения с различными коэффициентами нерегулярности к приведена в табл. 3. Критерием выбора метода схематизации является коэффициент нерегулярности исследуемого процесса нагружения к .

Таблица 3

Область применения методов схематизации

5. СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ СХЕМАТИЗАЦИИ

5.1. Функции распределения

Для оценки нагруженности и сопротивления усталости элементов машин и конструкций используют следующие функции распределения:

h (x_s) — распределение частот повторения x_s

H(x_s) — распределение накопленных частот повторения х_s;

F_э(x_s) — эмпирическая функция распределения;

F(x_s) — сглаженная эмпирическая функция распределения;

f(x_s) — эмпирическая функция плотности распределения.

Перечисленные функции распределения могут строиться для амплитуд х_а, приведенных амплитуд, размахов а, максимумов х_mах и минимумов х_min выделенных циклов. Функции распределения представляют в виде таблиц с числом интервалов m. Ширину интервала группирования случайной величины принимают равной или кратной ширине класса Δ. В таблицах распределений h(x_s) и H(x_s) указывают в циклах или полуциклах полученные частоты распределения. Примеры построения рядов распределений, графическая интерпретация функции F_э(x_s) и функции плотности распределение f_э(x_s) приведены в .

5.2. Расчет статистических характеристик распределений

Расчет статистических параметров распределений случайных величин, полученных в результате схематизации, проводят по формулам:

среднее выборочное значение случайной величины

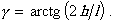;                                                                                         (14)

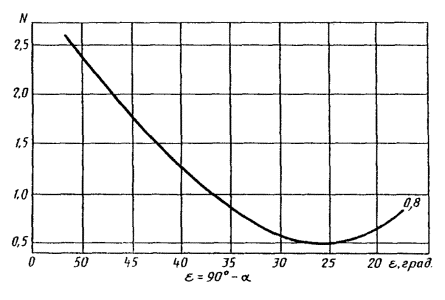
выборочная дисперсия

;                                                                              (15)

выборочное среднеквадратическое отклонение

;                                                                                              (16)

коэффициент вариации

,                                                                                         (17)

где h_sk— значение h (x_s) в k-м интервале.

ПРИЛОЖЕНИЕ 1
Обязательное
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ, ПРИМЕНЯЕМЫЕ В СТАНДАРТЕ

ПРИЛОЖЕНИЕ 2
Справочное
МЕТОД ПЕРЕСЕЧЕНИЙ ДЛЯ СХЕМАТИЗАЦИИ ПРОЦЕССОВ НАГРУЖЕНИЯ

Для числа пересечений отдельных уровней и числа максимумов и минимумов в классе i справедливо соотношение

|h_bi—h_bi-1| = |h() — h()|,                                                                 (1)

где h_вi — число пересечений верхней границы i-го класса восходящими или нисходящими ветвями процесса.

Для того чтобы воспользоваться уравнением (1), принимают следующие допущения:

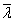,                                                                           (2)

 

Зная распределения h_вi с использованием соотношений (1) и (2), строят распределение h (x_max) и h (x_min) используя для выделения амплитуд принцип метода экстремумов (п. ), и на основании распределения h (x_max) и h (x_min) строят распределение амплитуд h (x_a)

.                                                           (3)

Экстремумы, попадающие в класс , не учитывают при построении распределения h (x_a), так как для них амплитуда меньше половины ширины класса Δ.

Для процесса, изображенного на чертеже, распределения h_bi, h (x_max), h (х_min) и h (x_a) приведены в таблице.

Схематизация процесса нагружения по методу пересечений

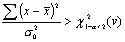
Распределения, полученные по методу пересечений

ПРИЛОЖЕНИЕ 3
Справочное
ПРИМЕР СХЕМАТИЗАЦИИ ПРОЦЕССА НАГРУЖЕНИЯ

Для процесса, изображенного на черт. 1, коэффициент нерегулярности к = 0,6. Для процессов, имеющих такой коэффициент нерегулярности, допускается применять любой из изложенных методов схематизации (см. настоящего стандарта).

В таблице приведены распределения, полученные при однопараметрической схематизации процесса разными методами. На черт. 2 приведена графическая интерпретация распределений. Следует отметить, что для данного процесса имеет место небольшое расхождение результатов схематизации по разным методам.

Распределения амплитуд, полученных по разным методам схематизации

Примечание. Распределения h (x_s) и Н(x_s) приведены для полуциклов.

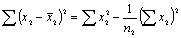
Черт. 1

1 — метод размахов; 2- метод «дождя»; 3 — метод экстремумов; 4- метод пересечений

Черт. 2

ПРИЛОЖЕНИЕ 4
Справочное
ПРИМЕРЫ СТАТИСТИЧЕСКОГО ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ СХЕМАТИЗАЦИИ

1. Распределение частот повторений h (x_s)

Функция h (x_s) представлена в табл. 1.

Таблица 1

Продолжение табл. 1

В первой строке таблицы указывают номера интервалов k; во второй — границы интервалов: x_вsk — верхняя граница, x_нsk — нижняя граница k-гo интервала; в третьей строке — середины интервалов —  в четвертой — частоты попадания случайной величины в k-й интервал — h_sk Если случайная величина попадает на границу интервала, суммирование осуществляют в интервале с большим номером.

Табл. 1 заполнена для амплитуд полуцикла процесса нагружения, изображенного на настоящего стандарта при схематизации по методу «дождя». Величины интервалов и классов совпадают.

2. Распределение накопленных частот повторений Н (x_s)

Вычисление функции H(x_s) по данным табл. 1 представлено в табл. 2. Накопленные частоты вычисляют по формуле

.                                                                                            (1)

 

Общее число циклов в блоке v₆ вычисляется по формуле

                                                                                     (2)

 

и составляет 24 цикла (по данным табл. 2).

Таблица 2

Функция накопленных частот

3. Эмпирическая функция распределения F_э (x_s)

Функция F_э (x_s) по тем же цифровым данным представлена в табл. 3. Значение функции F_э (x_s) определяет относительную частоту события x_s < X_s. Для вычисления F_эk используют формулу

.                                                                                       (3)

Таблица 3

Вычисление эмпирической функции распределения F_э (x_s)

По эмпирической функции распределения с использованием методов математической статистики, при необходимости, проводят подбор теоретического закона распределения.

4. Сглаженная эмпирическая функция распределения F(x_s)
эмпирическая функция плотности распределения j (x_s)

Построение F(x_s) показано на чертеже. На нормальную вероятностную бумагу наносят точки (x_sk, F_эk)из табл. 3, которые затем соединяют плавной кривой линией, изображающей функцию F(x_s). Значения F(x_s)приведены в табл. 4. В табл. 4 приведены значения функции плотности распределения j(x_s), которую строят как ступенчатую аппроксимацию функции F(x_s).

                                                                                        (4)

Таблица 4

Сглаженная функция распределения F(x_s) и функция плотности f(x_s)

Функция распределения F(x_s), представленная на нормальной вероятностной бумаге

+ — функция F_э(x_s),○ — функция F(x_s)

ПРИЛОЖЕНИЕ 5
Справочное
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАНДАРТА

Настоящий стандарт разработан на основе стандартов () и СССР (, ), а также с учетом новых разработок и опыта промышленности двух стран (-, -). Стандарт является унифицированным стандартом ГДР и СССР.

Рекомендация длительности реализации, как содержащей не менее 1000 экстремумов, основана на опыте ряда отраслей промышленности в СССР и согласуется с соответствующей рекомендацией ГДР, как обеспечивающей надлежащую точность оценок параметров функций распределения амплитуд напряжений.

Из многочисленных известных методов схематизации случайных процессов в стандарте основное внимание уделено группе методов, основанных на выделении полных циклов, а именно, методу полных циклов и методу «дождя». Эти методы дают практически одинаковые результаты и, по мнению большинства специалистов, являются наиболее обоснованными.

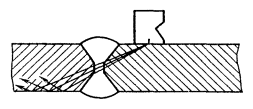
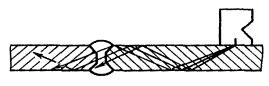
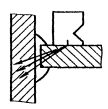
Если метод экстремумов приводит к схематизированному процессу более повреждающему, чем реальный, метод размахов — к менее повреждающему, то методы полных циклов и «дождя» занимают промежуточное положение и дают расчетные оценки долговечности, более соответствующие экспериментальным данным. Сущность методов заключается в том, что меньшие циклы рассматривают как наложенные на плавный ход нагрузки в одном направлении. На чертеже иллюстрируется явление наложения циклов.

Наложение циклов

а — фрагмент процесса нагружения; б- диаграмма «напряжение-деформация»

Для наглядности зависимость «напряжение-деформация» показана непропорциональной. Данный фрагмент образует две замкнутые петли гистерезиса или два цикла. Цикл 2-3-2 наложен на цикл с большей амплитудой 1-4-5. В свою очередь цикл 2-4-5 может быть наложен на еще больший цикл.

Особенность методов такова, что как бы далеко не располагались в реализации Х_mах и Х_min, наибольший размах a_max будет выделен.

При приведении асимметричных циклов к симметричным используется коэффициент влияния асимметрии цикла ψ_σ. В стандарте ГДР рекомендовалось для всех случаев принимать ψ_σ = 0,33. Однако, как показывают опытные данные для сварных и болтовых соединений, для других деталей с резкой концентрацией напряжений это значение является завышенным. Поэтому в настоящем стандарте рекомендовано принимать ψ_σ по рекомендации ГОСТ 25.504-82 для стальных деталей и по соответствующим справочникам для других материалов.

Выбор метода схематизации проводят по величине коэффициента нерегулярности к, равного отношению числа нулей процесса к числу экстремумов. Для процессов простой структуры, для которых к ≈ 1, все методы схематизации приводят практически к одинаковым результатам, поэтому для использования может быть рекомендован любой из них.

Для процессов сложной структуры, для которых к ≤ 1, рекомендуются методы полных циклов или «дождя», как обеспечивающие наиболее достоверную оценку уровня нагруженности.

Литература

1. ГОСТ 23207-78 «Сопротивление усталости. Основные термины, определения и обозначения».

2. ГОСТ 23604-79* «Надежность в технике. Статистическая оценка нагруженности машин и механизмов. Методы обработки данных о нагруженности. Общие положения.

3. Когаев В.П. Расчеты на прочность при напряжениях, переменных во времени. М., Машиностроение, 1977, 232 с.

4. Дмитриченко С.С., Полев В.А., Боровик А.П. Автоматизация расчета на ЭВМ долговечности элементов машин при случайном нагружении. «Вестник машиностроения», № 1, 1982, стр. 7-11.

5. Трофимов О.Ф., Злобин Б.Н. Статистический анализ измерений случайной нагруженности для оценки накопления усталостных повреждений. «Вестник машиностроения», № 10, 1969, стр. 3-5.

6. К.Н. Вöhmе. Beanspruchungskollektive und ihre Erwartenswahrscheinlichkeit als Grundlage zur Berechnung der Ausfallwahrscheinlichkeit von Bauteilen. «JFL-Mitteilungen», H 1/2, 1976.

7. F. Pfeiffer. Untersuchungen zum EinfluB regelloser Beanspruchungsfolgen auf die Bauteilermüdung «JFL — Mitteilungen», H, 1/2, 1976.

8. J. Dathe, D. Meisel und W. Weygandt. Die Schadigungsgrenze bei Kollektivbeanspruchung und ihre Berucksichtigung beim experimentellen Betriebsfestigkeitsnachweis. «JFL-Mitteilungen», H. 1/2, 1976.

9. F. Pfeiffer und K. Frintert. Zangzeitklassiergerät zur Ermittlung von repräsentativen Belastungskollektiven. «JFL-Mitteilungen», H. 1/2, 1976.

10. DDR-Standard TGL 36766. Schwingfestigkeit Ermüdungsprüfung von Werkstoffproben.

11. Hänel, G.Wirthgen. Die Berechnung der Dauerfestigkeit nach dem verfahren von Kogaev und Serensen. «JFL-Mitteilungen», H. 3, 1981.

12. DDR-Standard TGL 33787. Schwingfestigkeit Regellose Zeitfunktion Statidtische Auswertung.

13. Frank Lange und Fritz Pfeiffer. Statistisches Verfahren zur Auswertung von Betriebsbeanspruchungen auf der Basis der Bewertung geschlossener Hystereseschleifen («Rain-Flow») «IFL-MITT» (21), 1982, N 1.

14. Кагl-Нeinz Bohme. Auswertung von regellosen Zeitfunktionen nach geschlossenen Hystereseschleifen («Rain-Flow» mittels ProzeBrechners «IFL-MITT» (21), 1982, N 1.

15. F. Pfeiffer. Vergleichende Schwingfestigkeitsversuche an geschweiBten Proben bei Random-und-Blockbeanspruchung «IFL-MITT», 1981, N 2.

* С 1 июля 1986 г. действует методический документ (ИУС 8-86).